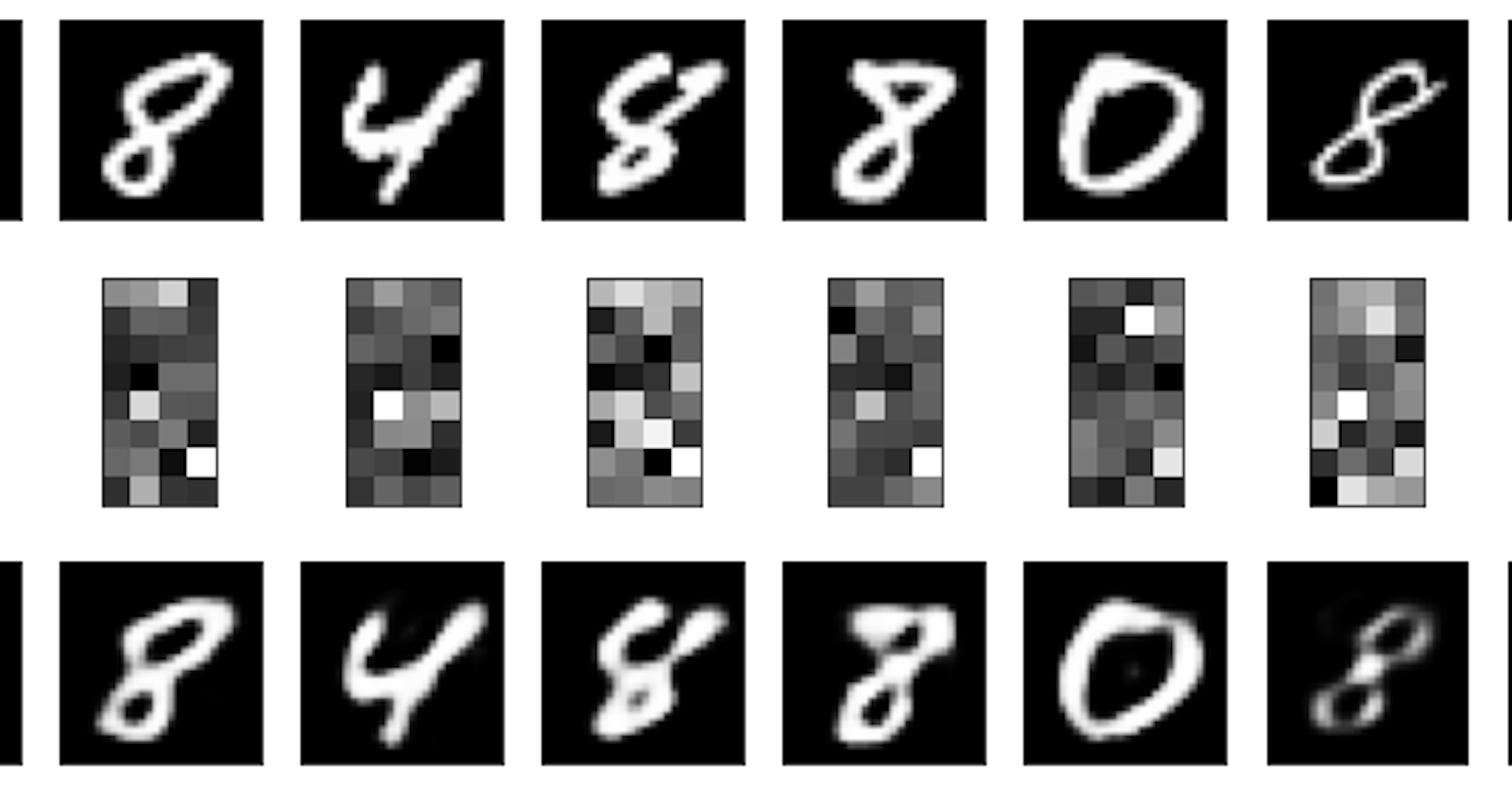An auto-encoder is a type of neural network that is able to learn a particular features of its input data without supervision. It encodes salient features of your input data using (typically) less dimensions, maintaining just enough to re-generate a fairly solid approximation of your original input. To make this point concrete, take the following set of numbers (if you're familiar with sequences, you'd recognise the Fibonacci sequence or 'Golden ratio') $$ 1,1,2,3,5,8,13,21,34 $$
The above can be represented by the following relation
$$ Tn = T(n-1) + (n-2) $$
In other words, every number in the sequence can be represented by a sum of the two preceding numbers. Therefore, given a suitable range for n and the above formula, the entire range of numbers can be reproduced from only the formula above. In the same way, and auto-encoder learns a compressed form or latent representation of your input data.
Learning Latent Representation
For a typical supervised learning problem, the outputs of your learning algorithm (in this case a neural network), is some useful label or value that can be derived from a combination of your input features, say, predicting the expected price of a house given location, age and number of bedrooms. This is done via the back-propagation algorithm, which essentially iteratively updates the weights of your network using the difference between the actual output for a given input and the value output by the network. In this way, your neural network is 'nudged' in the correct direction using the magnitude and sign of its output in relation to what the actual output is.
Auto-encoders on the other hand, use this expected output as the inputs of the network. This imposes a few constraints on the architecture of the given network. Firstly, the number of input nodes must be equal to the number of output nodes (no other configuration is possible if the outputs are expected to be equal to the outputs). Additionally, the number of internal nodes must be different from the number of input/output nodes. The reason for this is as follows, if there were 3 input and 3 output nodes in the given network, the weights for the internal nodes could all be set to 1, thereby in essence completely bypassing any effects of the network on the input data. The 'error' would always be zero, since this effectively multiplies the input data by one, and the main goal of encoding a representation of your input data is never achieved.
The final layer in your neural network is the decoder, this layer takes the latent representation of the input data learnt by the encoding layers, and attempts to reconstruct the input using only this learnt representation
Coding using TensorFlow
We'll be using TensorFlow's functional API to build a very simple auto-encoder in Python for the MNIST dataset. We first start by importing TensorFlow, and defining our input layer. The shape of this input layer must match the number of inputs we have per input sample, in this case, a single MNIST image is 784 pixels, therefore we have a shape of (784,)
import tensorflow as tf
inputs = tf.keras.layers.Input(shape=(784,))
We then create our Dense layers. The first dense layer has 32 units, as we attempt to encode or 'compress' our original input down to this size.
encoder = tf.keras.layers.Dense(32, activation='relu')(inputs)
Our decoder on the other hand, has the same shape as our inputs for reasons explained above, and takes the encoder layer as its input. If you're unfamiliar with the way the TensorFlow functional API works, see here
decoder = tf.keras.layers.Dense(784, activation='sigmoid')(encoder)
Finally, the autoencoder model is set up for the purposes of learning your encoded input data. Note that we also set up a second model with the encoder as its output, this is so that we can visualise what our model has learnt from the input data
encoder_model = tf.keras.Model(inputs=inputs, outputs=encoder)
autoencoder_model = tf.keras.Model(inputs=inputs, outputs=decoder)
We compile our model using the Adam optimizer, with a loss type of binary-crossentropy. Since our 'labels' are our input data, a binary loss function would account for match vs not-match for every single input value.
autoencoder_model.compile(
optimizer=tf.keras.optimizers.Adam(),
loss='binary_crossentropy')
The above gives rise to the following model architecture, which was generated using tf.keras.utils.plot_model

Examining The Output
After training on the input data, the following is output from our model. The first line shows the original input data, the second row is the output from our encoder_model, which shows the latent representation learnt by our network, and finally, the last row shows the decoder's attempted reconstruction using the latent representation used.

See my Github for a full overview of the data loading process. These notebooks are a collection of labs from the DeeplearningAI Generative Deep Learning course on Coursera
References
The MNIST Database of Handwritten Digit Images for Machine Learning Research